Equatorial Bulge

An equatorial bulge is a difference between the equatorial and polar diameters of a planet, due to the centrifugal force exerted by the rotation about the body's axis. A rotating body tends to form an oblate spheroid rather than a sphere.

On Earth

The Earth has a rather slight equatorial bulge: it is about wider at the equator than pole-to-pole, a difference which is about 1/298 of the equatorial diameter. If the Earth were scaled down to a globe with diameter of 1 meter at the equator, that difference would be only 3 millimeters. While too small to notice visually, that difference is still more than twice the largest deviations of the actual surface from the ellipsoid, including the tallest mountains and deepest oceanic trenches.

The rotation of the earth also affects the sea level, the imaginary surface that is used to measure altitudes from. This surface coincides with the mean water surface level in oceans, and is extrapolated over land by taking into account the local gravitational potential and the centrifugal force.

The difference of the radii is thus about 21 km. An observer standing at sea level on either pole, therefore, is 21 km closer to Earth's center than if standing at sea level on the Equator. As a result, the highest point on Earth, measured from the center and outwards, is the peak of Mount Chimborazo in Ecuador rather than Mount Everest. But since the ocean also bulges, like Earth and its atmosphere, Chimborazo is not as high above sea level as Everest is. Similarly the lowest point on Earth, measured from the center and outwards, is the Litke Deep in Arctic Ocean rather than Challenger Deep in Pacific Ocean. But since the ocean also flattens, like Earth and its atmosphere, Litke Deep is not as low below sea level as Challenger Deep is.

More precisely, the surface of the Earth is usually approximated by an ideal oblate ellipsoid, for the purposes of defining precisely the latitude and longitude grid for cartography, as well as the "center of the Earth". In the WGS-84 standard Earth ellipsoid, widely used for map-making and the GPS system, the radius of the Earth is assumed to be at the equator and center-to-pole; meaning a difference of in the radii and in the diameters, and a relative flattening of 1/298.257223563. The sea level surface is much closer to this standard ellipsoid than the surface of the solid Earth is.

The equilibrium as a balance of energies

Gravity tends to contract a celestial body into a sphere, the shape for which all the mass is as close to the center of gravity as possible. Rotation causes a distortion from this spherical shape; a common measure of the distortion is the flattening (sometimes called ellipticity or oblateness), which can depend on a variety of factors including the size, angular velocity, density, and elasticity.

A way for one to get a feel for the type of equilibrium involved is to imagine someone seated in a spinning swivel chair and holding a weight in each hand; if the individual pulls the weights inward towards them, work is being done and their rotational kinetic energy increases. The increase in rotation rate is so strong that at the faster rotation rate the required centripetal force is larger than with the starting rotation rate.

Something analogous to this occurs in planet formation. Matter first coalesces into a slowly rotating disk-shaped distribution, and collisions and friction convert kinetic energy to heat, which allows the disk to self-gravitate into a very oblate spheroid.

As long as the proto-planet is still too oblate to be in equilibrium, the release of gravitational potential energy on contraction keeps driving the increase in rotational kinetic energy. As the contraction proceeds, the rotation rate keeps going up, hence the required force for further contraction keeps going up. There is a point where the increase of rotational kinetic energy on further contraction would be larger than the release of gravitational potential energy. The contraction process can only proceed up to that point, so it halts there.

As long as there is no equilibrium there can be violent convection, and as long as there is violent convection friction can convert kinetic energy to heat, draining rotational kinetic energy from the system. When the equilibrium state has been reached then large scale conversion of kinetic energy to heat ceases. In that sense the equilibrium state is the lowest state of energy that can be reached.

The Earth's rotation rate is still slowing down, though gradually, by about two thousandths of a second per rotation every 100 years. Estimates of how fast the Earth was rotating in the past vary, because it is not known exactly how the moon was formed. Estimates of the Earth's rotation 500 million years ago are around 20 modern hours per "day".

The Earth's rate of rotation is slowing down mainly because of tidal interactions with the Moon and the Sun. Since the solid parts of the Earth are ductile, the Earth's equatorial bulge has been decreasing in step with the decrease in the rate of rotation.

Effect on gravitational acceleration

Because of a planet's rotation around its own axis, the gravitational acceleration is less at the equator than at the poles. In the 17th century, following the invention of the pendulum clock, French scientists found that clocks sent to French Guiana, on the northern coast of South America, ran slower than their exact counterparts in Paris. Measurements of the acceleration due to gravity at the equator must also take into account the planet's rotation. Any object that is stationary with respect to the surface of the Earth is actually following a circular trajectory, circumnavigating the Earth's axis. Pulling an object into such a circular trajectory requires a force. The acceleration that is required to circumnavigate the Earth's axis along the equator at one revolution per sidereal day is 0.0339 m/s². Providing this acceleration decreases the effective gravitational acceleration. At the Equator, the effective gravitational acceleration is 9.7805 m/s². This means that the true gravitational acceleration at the Equator must be 9.8144 m/s² (9.7805 + 0.0339 = 9.8144).

At the poles, the gravitational acceleration is 9.8322 m/s². The difference of 0.0178 m/s² between the gravitational acceleration at the poles and the true gravitational acceleration at the Equator is because objects located on the Equator are about further away from the center of mass of the Earth than at the poles, which corresponds to a smaller gravitational acceleration.

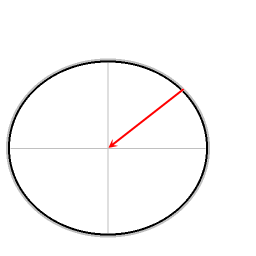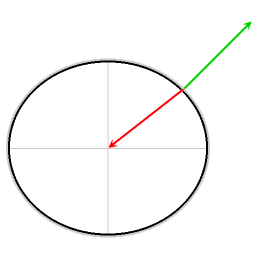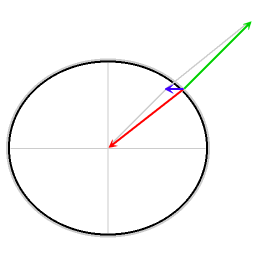
In summary, there are two contributions to the fact that the effective gravitational acceleration is less strong at the equator than at the poles. About 70% of the difference is contributed by the fact that objects circumnavigate the Earth's axis, and about 30% is due to the non-spherical shape of the Earth.

The diagram illustrates that on all latitudes the effective gravitational acceleration is decreased by the requirement of providing a centripetal force; the decreasing effect is strongest on the Equator.

Effect on satellite orbits

The fact that the Earth's gravitational field slightly deviates from being spherically symmetrical also affects the orbits of satellites through secular orbital precessions. They depend on the orientation of the Earth's symmetry axis in the inertial space, and, in the general case, affect ''all'' the Keplerian orbital elements with the exception of the semimajor axis. If the reference ''z'' axis of the coordinate system adopted is aligned along the Earth's symmetry axis, then only the longitude of the ascending node Ω, the argument of pericenter ω and the mean anomaly ''M'' undergo secular precessions.

Such perturbations, which were earlier used to map the Earth's gravitational field from space, may play a relevant disturbing role when satellites are used to make tests of general relativity because the much smaller relativistic effects are qualitatively indistinguishable from the oblateness-driven disturbances.

Formulation

The flattening coefficient $f$ for the equilibrium configuration of a self-gravitating spheroid, composed of uniform density incompressible fluid, rotating steadily about some fixed axis, for a small amount of flattening, is approximated by:
$f = \frac = \frac \frac = \frac \frac$

where
*$G$ is the universal gravitational constant,
*$a$ is the mean radius,
*$a_e = a\, (1 + \tfrac)$ and $a_p = a\,(1 - \tfrac)$ are respectively the equatorial and polar radius,
*$T$ is the rotation period and $\omega = \tfrac$ is the angular velocity,
*$\rho$ is the body density and $M \simeq \tfrac \pi \rho a^3$ is the total body mass.

Real flattening is smaller due to mass concentration in the center of celestial bodies.

See also

*
*Clairaut's theorem (gravity)
*Earth's gravity
*Planetary flattening

References

{{DEFAULTSORT:Equatorial Bulge
Planets
Geodesy
Topography